
Some Basic Statistics Concepts
Get yourself tooled up on some of the basics of data analysis
Census or Sample?
We're all aware of the idea of a census. Throughout the world, governments want to know as much as they can about the people whom they govern and ask questions about everyone in the country. For us statisticians, however, the definition is wider: it's a study of every member of any population: every member of a sports club, the bolts produced in one day in a factory, the students taking an examination. By convention, we called the population in a study N.
When we take measures of a population N, we are deriving parameters, such as the mean (μ) or variance (σ²).
Examples of parameters would be the percentage of the electorate who voted for a particular candidate, or the median salary of the workers in a business.
But we do not always have the complete data to hand, so instead we use a sample of the data (n) to estimate the parameters. These are sample statistics, such as the sample mean (x̅) and variance (s²).
Inferential statistics is the use of sample statistics to provided estimates about the population.
This is done by making use of sampling methods and the applying appropriate statistical techniques, which will also provide measures of the accuracy of our estimates.

Averages - Measures of Central Tendency
Mean:
The (arithmetic) mean of a sample (x̅) is used to estimate the mean of the population (μ). Simply put, it is the sum of the values divided by the number of samples (n): Suppose x1, x2, x3, ... , xn be n observations of a data set, then the mean of these values is:
x̅=∑xi/n
where
xi = ith observation, 1 ≤ i ≤ n
∑xi = Sum of observations
n = Number of observations
Median:
the (n+1)/2th number, when examined in order of their value.
When n is an even number, the median is the value halfway between those of the n/2th and the (n+2)/2th numbers (e.g. if 8 numbers, the median is the midway value between the 4th and the 5th values.
Mode:
the most popular value.

Measures of spread
How similar are all the observed values of a particular variable? Are they all nearly identical; are there a few values that are different (outliers); or are these values quite different throughout the dataset? We examine this by measuring the spread or dispersal of these data*.
*It is common, in statistics, to be precise in definitions, so one data item (a datum) is singular, more than one (data) is plural.
Variance and standard deviation:
How far apart are the set of individual values from the mean? Taking every value, measure its distance from the mean and sum these differences will, common sense tells you, sum to zero. So instead, square the differences to give them all positive values. The larger the differences, the greater the total number. And, of course, the larger the dataset, the greater the total number, so dividing the total by the population standardises the value. This formula is the variance. For a population, this is:
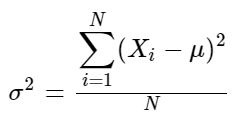
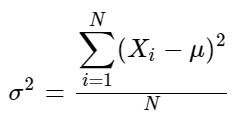
and for a sample:
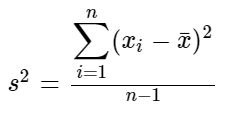
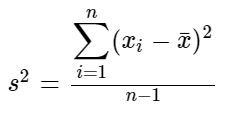
The sample variance is divided by the sample population minus one. This is Bessel's correction. Without delving further into theory, it is an adjustment to deal with the bias in the sample. The value of the variance is increased accordingly.
As the variance is a sum of squares, the standard deviation, which is the square root of the variance, brings the statistic to the same dimension of the other measures of dispersal, and so more appropriate.
The standard deviations are denoted by σ and s.
Range:
This is simply the difference between the largest and the smallest value
Interquartile range:
Where the median is the value of the value in the middle of the data, arranged in order, the quartiles are at the quarter and three-quarter positions, Q1 and Q3 respectively.
The interquartile range is the difference between Q1 and Q3.
A useful way that these statistics can be displayed graphically is by using a box plot, sometimes called a box and whisker plot.
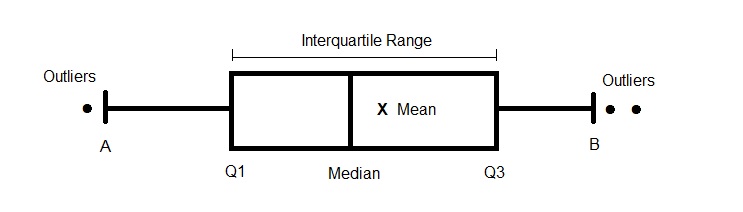
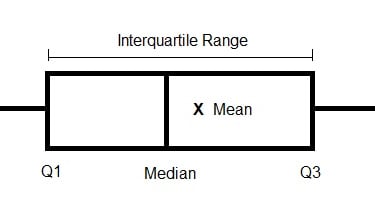
A typical box plot is shown above - but not all box plots show the same information.
This one gives a snapshot of your variable, showing how tight, or otherwise, the values are. You can see the range of half of the data by the shape of the interquartile range, and observe that there are, in this example, three outliers outside points A and B. These points are determined by multiplying the value of the interquartile range by 1.5; point A is Q1 minus that value, point B plus the value. Other box plots replace A and B by the 5th and 95th percentiles (calculated in a similar fashion to the median, Q1 and Q3. Others may dispense with the outliers and use the minimum or maximum value.
